内角和公式怎么算，正多边形的内角和公式怎么算！

投稿用户 • 2022年11月2日 pm11:26 • 范文大全 • 阅读 2791

在2018年下半年教通云翔老师班的数学时（通老师是班主任），大量讲过八年级上册第十一章的三角形中的多边形内角和问题，为了锻炼学生的思维能力，多边形的内角和是一个不可多得的训练方向。在这些大量训练的时候，发现在教这一章的三角形内角和与三角形外角和所得出的一些做题模型，例如筝形、箭形等模型结论与多边形内角和及外界和像是关系不大。特别是多边形内角和强调的是角度转化及利用多边形内角和公式，三角形内外角和引出了多边形内角和公式，三角形内角和与外角和到最后也是强调公式而忘记三角形内角和与外角和的探索过程了。

当有这个问题的发现时，学生已经练习了大量的多边形内角和与外角和的求解。直到有天午自习一个孩子没睡觉跑到我面前说：老师，你能给我讲讲多边形内角和与外角和的其他求解方式吗？你现在讲的方法，我不太会。我想了下，觉得常规方法不就挺好吗，锻炼思维，还能培养转化意识。我让他给我说说他那不会，才知道他一直卡在了角的相互转化上了。我让他回去，让我思考一个夜晚。

当天下午，我就开始大量地收集多边形的内角和与外角和相关的习题，一道道的去求解，做一会就赶紧去总结。做了一下午，感觉什么收获都没有，水但是喝了很多，在明德楼五楼的办公室只有我和我的师傅甘海水老师在那坐，原因很简单，一是僻静；二是人少可以抽烟。在快放学的时候，我看见我写的详案了——关于三角形内角和与外角和小专题中的箭形、筝形等模型及结论，就这一眼我醒悟了，我向师傅甘老师求教，他让我试试我说的方法是不是普遍适用，如果是普遍适用就讲给学生听。回到家又结合教案进行相关的汇总与归纳加上题型的普适性实验，结果那天熬到了凌晨五点多钟，做个早餐，送完孩子，就屁颠屁颠的跑学校了，脚步很沉重，但眼镜却是发亮的，用学生的话说是“发现财宝，想偷的眼神，贼亮！”

下面是两届教案整理：

拼图法的知识储备：

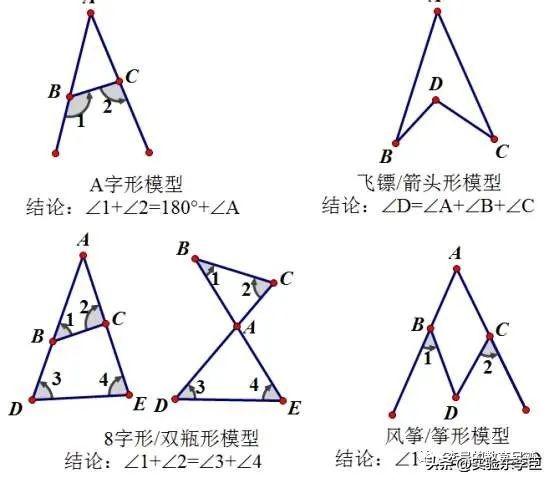
?以上的模型在三角形的内角和及外交中都是必须讲的，当然不能说你没讲就不对，这是不合适的，将与不讲在于教师意愿也在于学生的接受能力，接受能力强的学生就不应该先将这些模型，而是让他们在锤炼自己的思维能力后再去将这个总结性的知识，但也是引导学生去探索并发现，最后总结。接受能力差点的学生是可以先讲这个的，是有取巧了，只能说接受能力差也可以考高分吧，强的是学生的技能而不是学生的思维，这是有前提的，前提是你教的孩子得有进取心，不然他连技巧也不会记！或是你的内心足够强大到压服所有学生！

有了这些储备后，就可以做题了。

例如图1所示，求解∠***+∠B+∠C+∠D+∠E=

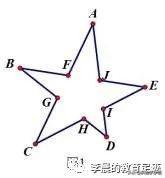
〖拼图法〗把图一分解成两种模型图的拼图，再加上对应模型结论，答案秒出！当然啦，大题解答也是可以直接套用的！（不用讲，有基础的是不是已经会了！你很牛！）

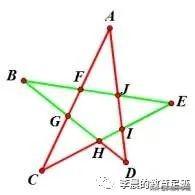
大题解答技巧如下：

解：如

上图所示：三角形BHE中∠CHD=∠B+∠E

在筝形中∠CHD=∠***+∠C+∠D

所以可以得出：∠***+∠C+∠D+∠B+∠E=180°

当然，你让不让学生用或是改卷老师认不认可，与本人无关了啊！我已经不教数学了！但是对于填空题或是思维不是特别苛刻的改卷老师，你是满分哦！我看好你！

由此我们发现拼图法是不是很好用，写在最后吧!在我2022年的暑假看新的教辅资料的时候发现有部分数学资料已经有拼图法的解题方法了，我也得遵循学术界的基本潜规则——谁先发表谁就有话语权及所有权！

所以，在2018年的时候，我还给学生开玩笑说这是“李氏拼图法”，在2021年教第二届数学的时候也说过，那么当别人也发现并发表之后，“李氏拼图法”就是笑谈了，当然我也不会认为发现没有意义，发现的意义就在于我们还知道去归纳去探索！还知道去学生的诉求，以及直追数学之根本，数学就是要用最优解去解决问题的，不是吗！

最后给展示五角星图内角和的变形题吧（不是原创题，最早发现与《53天天练（2018年版）》，当然《典中点》中该题型也很多！）。想想还是算了吧，我都不教数学了，再把变形题附上去，不是难为自己吗，是不是正解，那就少接触几何画板，要不然这个下午又是在电脑前制作几何图了！

详案写于2018年9月及2021年9月（已经被别人借走了，用于何处，不可考证！）

文章整理修改于2022年9月29日

............试读结束............

查阅全文加微信：3231169

如来写作网：gw.rulaixiezuo.com（可搜索其他更多资料）

本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容，请发送邮件至 3231169@qq.com 举报，一经查实，本站将立刻删除。
如若转载，请注明出处：https://www.gongwencankao.com/3699.html

内角和公式怎么算，正多边形的内角和公式怎么算！

相关推荐